This manual provides a description of the formulae and computations performed
by the Single-Dish Exposure Time Calculator (ETC) considering the different
observing modes and observing strategies.
Specific characteristics related to observations with Medicina or SRT are
mentioned in the text when appropriate.
The ETC output for the SRT now includes a note on the nodding observing
strategy.
With respect to position switching, nodding doubles the useful time on source
in the same cycle time. More info on this observing technique can be found in
Spectroscopic
observations with the SRT using the Nodding technique.
Changed computations for OTF Cross Scan to match the DISCOS observing system
requirements. Now one Cross Scan is considered as composed by two crosses
(i.e. four subscans) instead of one, see
On-The-Fly Cross Scan
computations for details.
Improved MathJax support.
Improved documentation regarding how the ETC deals with
multi-feed receivers.
-
Cross Scan computations are no more done over a HPBW area. The sensitivity
associated to a single subscan coincides with the one calculated, using the
plain radiometer formula, considering an integration time equal to the
sampling interval. This way, it
practically represents the RMS noise that will characterize the single
subscan. When the user provides the desired final sensitivity, the
ETC computes how many subscans must be integrated in order to reach it,
subsequently estimating the total required observing time including the
a priori known overheads.
Addiotionally, due to the presence of polarized RFI or other sources of
asymmetry between the LCP and RCP data, computations are conservatively
made taking into account a single IF. See the On-The-Fly Cross Scan section
for further details on calculations.
-
Units for sensitivity and source flux (for OTF map computations) can now
be expressed in units of mJy or Kelvin. The same unit is expected for both
quantities.
If the selected unit is Kelvin, we assume that the input source flux
correspond to \(T_{A}^{*}\) that is the antenna temperature outside the
atmosphere. The source flux is used only to compute the expected
Signal-to-Noise Ratio. The measured flux is computed by correcting
\(T_{A}^{*}\) for the atmospheric effects as:
\(T_{A} = T_{A}^{*} \times e^{\frac{-\tau}{sin(El)}}\) .
-
A more accurate evaluation of \(T_{sys}\) in K bandis performed, see the
System Temperature section.
-
Total Power: the band-limited noise is now computed using the radiometer
formula corrected for an empirically-evaluated "real world" factor, in
order to better represent a real-life scenario. Measurement campaigns
have in fact shown that the larger bandwidths may account for a
difference between the expected and the measured sensitivity as high as a
factor of two.
The ETC currenlty applies a RealWorld=2 for bandwidths larger than 250 Mhz.
The value of the RealWorld parameter is listed in the ETC output. See
Basic Formulae
for further details.
-
Spectropolarimetry: the spectral rebinning that may be performed during the
data processing phase is now simulated via the Rebin term, see the
description of the spectral cases in the
Basic Formulae
section.
-
The ETC output now also lists the beam efficiency for the selected
receiver.
Basic Formulae
System Temperature
Receiver Gain
Multi-feed Receivers
Radiometer Formula + Position Switching computations
Input parameters
Position Switching computations
Nodding
Output Parameters
On-The-Fly Cross Scan computations
Input parameters
Output parameters
On-The-Fly Map computations
Input parameters
Output parameters
Confusion Noise computations (contribution by V. Vaccca)
The basic formula for the ETC is the so-called radiometer formula:
|
$$t_{TOT} = \left(\frac{T_{sys}}{G \; s_{TOT}}\right)^2
\frac{1}{totBand}$$
|
where:
\(T_{sys}\) = system temperature (\(^{\circ}\)K)
\(G\) = gain (K/Jy)
and:
\(s_{TOT}\) = \(s_{TOT}^{input}/RealWorld\) = input sensitivity (converted to Jy) corrected by the \(RealWorld\) factor.
\(RealWorld\) is a numerical factor to take into account the observed discrepancy
between the expected and measured sensitivity depending on the bandwidth.
Observational data from Medicina and SRT show that, for large bandwidths
(empirically, larger than 250 MHz), the actual sensitivity is twice the
theoretical one from the radiometer formula.
The term \((s_{TOT}/RealWorld)\) is the expression of the following statement:
if one wants to know how much time it takes to actually reach a measured
sensitivity \(s_{TOT}\), the ETC must compute how much time it takes to reach
a theoretical sensitivity which is RealWorld times better than \(s_{TOT}\).
The term \(totBand\) has different meanings depending on the observing mode:
| Continuum (no polarimetry): |
\(totBand = \Delta \nu \; N_{IF}\)
|
| Spectroscopy (no polarimetry): |
\(totBand = \Delta \nu_{ch} \; N_{IF} \; Rebin\)
|
| Spectropolarimetry: |
\(totBand = 2 \; \Delta \nu_{ch} \; Rebin\)
|
where:
\(\Delta \nu \) = instrument bandwidth (Hz).
\(\Delta \nu_{ch} \) = spectroscopic channel bandwidth (Hz).
\(N_{IF}\) = number of output IF
\(Rebin\) = multiplying factor to simulate the spectral rebinning that may be
applyied during the data processing.
In the following computations, \(totBand\) assumes the value corresponding
to the user-selected observing mode.
System temperature for receivers working below 22 GHz
is considered to be a function of the source elevation only.
The user gives in input to the ETC the elevation at which the observation
will be conducted (see next paragraphs) and the ETC selects among tabulated
values the \(T_{sys}\) best matching the user-selected elevation.
When observing at 22 GHz we consider also a dependence
on atmospheric conditions through the formula:
|
\(T_{sys} = T_{ric} + \eta_{f}T_{atm}(1 - e^{\frac{-\tau}{sin(El)}}) +
(1 - \eta_{f}) T_{gnd}\)
|
where:
\(T_{ric}\) = receiver temperature (K)
\(\eta_{f}\) = feed efficiency, characteristic of each telescope
\(T_{atm}\) = atmospheric brightness, expressed as a temperature (K)
\(T_{gnd}\) = ground level temperature (K).
\({\tau}\) = atmospheric opacity
\(El\) = source elevation at the epoch of the observation.
Opacity and \(T_{gnd}\) are tabulated values varying with season
(Spring, Summer, Autumn, Winter) and are selected on the basis of the ETC
user input parameters. We use
\(\eta_{f}=0.986\) and \(\eta_{f}=0.9\) respectively for Medicina and SRT.
For Medicina we use tabulates values also for \(T_{atm}\), while for SRT the
following approximated formula is used:
|
\(T_{atm} \approx 0.683 T_{gnd} + 77.919\)
|
Receiver gain is computed differently for SRT and Medicina telescopes.
For Medicina, gain is computed by means of the polynomial formula:
\(G(x) = DPFU \times (ax^2 + bx +c)\) K/Jy,
where x is the source elevation and DPFU, a, b, and c are
tabulated values for each receiver.
In the case of SRT, gain is approximately constant at any
elevation, thus each receiver is characterized by a single gain value which is
used by the ETC without the need to apply the above formula.
ETC computations are done always considering one feed, even if a multifeed
receiver (like the K-band one at SRT and Medicina) is selected.
Multi-feed receivers offer a variety of observing strategies (from nodding
to continuous on-the-fly mapping etc.) that can be hardly represented in a
simple and effective way in the Exposure Time Calculator. It is
therefore left to the user the adjustment of the results to take into account
the adopted multi-feed observing strategy.
Computations in this case are done by simply applying the radiometer
formula to the user-selected values.
In addition, an example case of
Position Switching observation is evaluated, assuming to perform an
ON-OFF-OFF-ON cycle. The following Figure illustrates the geometry
of a Position Switching observation.

The ON position corresponds to the
on-source one, while the OFF observation is executed at a nearby position on
the empty sky. The OFF position is assumed to be at a distance of 5 beamsizes
from the ON one. An ON-OFF-OFF-ON sequence is assumed to minimize the time
requested to move the telescope between consecutive positions.
ETC computations are done always considering one feed, even if a multifeed
receiver (like the K-band one at SRT and Medicina) is selected.
The user provides in input:
1) the desired sensitivity \(s_{TOT}\) (mJy) OR
the desired time \(t_{TOT}\) (sec).
CASE A: GIVEN \({\bf s_{TOT}}\) COMPUTE \({\bf t_{TOT}}\)
The radiometer formula is used to compute the exposure time needed to
reach a given sensitivity:
|
$$t_{TOT} = \left(\frac{T_{sys}}{G \; s_{TOT}}\right)^2
\frac{1}{totBand}$$
|
CASE B: GIVEN \({\bf t_{TOT}}\) COMPUTE \({\bf s_{TOT}}\)
By reverting the radiometer formula:
|
$$ s_{TOT} = \left(\frac{T_{sys}}{ G}\right) \;
\sqrt{\frac{1}{totBand \; t_{TOT}}} $$
|
An example case for Position Switching observations is also computed as a
particolar case for the radiometer formula mode.
For Position Switching computations we assume that the four exposures in the
cycle will be combined as
[(ON\(_1\)-OFF\(_1\)) + (ON\(_2\)-OFF\(_2\))]/2 to get the final result. We also assume
that the time spent on each position is the same (\(t_{ON} = t_{OFF}\)), that
measurements are independent and that they have identical uncertainties.
The r.m.s. on the frame resultant from one (ON-OFF) subtraction is:
|
$$ s_{ON-OFF} = \sqrt{s_{ON}^{2} + s_{OFF}^2} =
\sqrt{2} \times s_{ON} $$
|
The r.m.s. on the frame resultant from the average of the two (ON-OFF)
subtractions, i.e. the r.m.s. of one ON-OFF-OFF-ON cycle is, according to the
error propagation for the mean:
|
$$ s_{cycle} = \sqrt{\frac{1}{2} \times s_{ON-OFF}^{2}} =
\sqrt{\frac{1}{2} \times (\sqrt{2} \times s_{ON})^{2}} = s_{ON} $$
|
A) If the user-selected input sensitivity is intended to be reached
in one
complete ON-OFF-OFF-ON cycle of Position Switching, i.e. \(s_{cycle} = s_{TOT}\),
\(t_{cycle}\) is computed as:
|
$$ t_{cycle} = 2 \times (t_{ON} + t_{OFF} + t_{shift}) + t_{prep} $$
|
The value of \(t_{ON}=t_{OFF}\) is computed by obtaining \(s_{ON}\) from the above
equation for \(s_{cycle}\) and applying the:
|
$$ t_{ON} = \left(\frac{T_{sys}}{G}\right)^2 \frac{1}{s_{ON}^2
\times totBand} $$
|
The other terms in \(t_{cycle}\) are: \(t_{prep}\), which is the instrument setup
time, {\bf currently set to zero for Medicina and SRT telescopes (as of Dec.
2014)} and \(t_{shift}\), the slewing time needed to move from one position to
the next. The value for \(t_{shift}\) is computed by means of the uniformly
accelerated motion formula assuming that the OFF position is 5 beamsizes away
from the ON position:
|
$$ t_{shift} = \sqrt{(5 \times HPBW) \; \frac{2}{MaxAcc}} $$
|
The value of the maximum acceleration is set inside the ESCS/Nuraghe
CommonDataBase (CDB).
For Medicina and SRT we consider the maximum acceleration \(MaxAcc\) to be
\(0.4 \,\, {\rm deg/ sec}^2\) and \(0.25 \,\, {\rm deg / sec}^2\) respectively.
B) In the opposite case in which the user-selected input exposure time
is intended to be used for the execution of a complete ON-OFF-OFF-ON cycle of
Position Switching, \(t_{cycle} = t_{TOT}\). The value for \(s_{ON}\) to be
inserted
in the \(s_{cycle}\) equation is evaluated as:
|
$$ s_{ON} = \left(\frac{T_{sys}}{G}\right) \;
\sqrt{\frac{1}{totBand \times t_{ON}}} $$
|
where \(t_{ON}\) is obtained by reverting the equation for \(t_{cycle}\):
|
$$ t_{ON} = [ t_{cycle} - (2 \times t_{shift}) - t_{prep}]/ 4 $$
|
The ETC output for the SRT now includes a note on the nodding observing
strategy.
With respect to position switching, nodding doubles the useful time on source
in the same \(t_{cycle}\). More info on this observing technique can be found in
Spectroscopic
observations with the SRT using the Nodding technique.
When selecting the radiometer formula computations, the following
parameters are given in output:
-
Receiver gain and system temperature, taken from tabulated values for the
selected receiver.
- Actual elevation used for computations: this parameter may sligthly
differ from the user-selected one. Values for \(T_{sys}\) are tabulated
at different values of the elevation, typically every 5 degrees. Among the
tabulated values, the ETC looks for the \(T_{sys}\) which was measured at the
elevation closest to the user-selected one.
- Estimate of the Confusion Noise at the selected frequency (not implemented
for Medicina).
- Time on Source (sec) or Sensitivity (mJy) computed according with the
selected input values.
- Example case for Position Switching Observations, in which an estimate of
the total time needed to complete an ON-OFF-OFF-ON cycle is given. This
estimate currently does not include the slewing time between positions and
the system setup time.
- A note and reference on nodding is given.
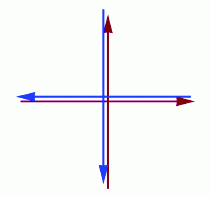
OTF Cross Scans acquired with the DISCOS observing system at the INAF radio
telescopes are by default composed by two crosses, i.e. four subscans.
Each scan is thus composed by four orthogonal subscans, to form two crosses.
The source is assumed to be coincident with the intersection of the
cross. Data acquisition is continuously performed in short time intervals
during the scan.
To reach a given sensitivity over a position many consecutive
Cross Scans may be required.
An example of the Cross Scan geometry is shown in the following Figure, where
two consecutive crosses are executed over the same position (the small
displacement between the blue and red crosses is for visualization
purposes) and each arrow represent a subscan.
ETC computations are done always considering one feed, even if a multifeed
receiver (like the K-band one at SRT and Medicina) is selected.
For OTF Cross Scan computations the user provides in input:
1) the length of each subscan: \(subscanLength\) (expressed in units of HPBW for
the selected receiver);
2) the constant scan speed at which the telescope moves while scanning:
\(scanSpeed\) (arcmin/sec, equivalent to deg/min);
3) the time interval between two subsequent data samples:
\(sampleInterval\) (sec);
4) the desired sensitivity to be reached at the source position, i.e. the
final sensitivity
\(s_{TOT}\) obtained by integrating a suitable n. of Cross Scans,
OR the total time \(t_{TOT}\) one wants to observe executing OTF Cross
Scans.
IMPORTANT NOTES:
1) In our computations, the sensitivity associated to a single subscan
coincides with the one calculated, using the plain radiometer formula,
considering an integration time equal to the sampling interval. This way, it
practically represents the RMS noise that will characterize the single
subscan. When the user provides the desired final sensitivity, the ETC
computes how many subscans must be integrated in order to reach it,
subsequently estimating the total required observing time - as it includes
intra-subscan and inter-subscan dead times (known a priori). Conversely, if
the user provides a time interval and wants to know to which sensitivity it
corresponds to, such time is intended as the total duration of the
observation, and the ETC computes how many subscans can be executed in that
time range, estimating the sensitivity reached by integrating them.
Those users who plan to employ the CAP (Cross-scan Analysis Pipeline) tool,
made available by INAF, must take into account that it separately performs
flux density measurements on each scan direction (e.g. separately
integrating RA scans and Dec scans, then computing the weighted average of
the two measurements). This way, the actual integration time associated to
the final measurement is half the total time, and the sensitivity drops by a
\(\sqrt{2}\) factor. Cross-scans are necessary in order to accurately assess the
pointing offset and correct the flux density measurements accordingly.
2) Due to the presence of polarized RFI or other sources of asymmetry
between the LCP and RCP data, computations conservatively take into account
a single IF. If the data quality allows for the integration of LCP and RCP
acquisitions, thus doubling the integration time, the actual sensitivity
will improve by a factor of \(\sqrt{2}\). As far as Total Power acquisitions are
concerned, the single-IF scenario is not infrequent.
3) Due to the need to make some approximation (f.i. the Cross Scan geometry
requires the total number of subscans to be a multiple of four),
the effective total sensitivity or the effective total time
are re-computed,
starting from the desired ones and taking into account the observing setup.
Effective values may slightly differ from the input values.
4) Given the observing constraints at the telescopes, sensitivity and time
are computed considering always a minimum number of one Cross Scan
(i.e. 4 subscans).
CASE A: GIVEN \({\bf s_{TOT}}\) COMPUTE \({\bf t_{TOT}}\)
The total time \(t_{TOT}\) needed to reach the desired sensitivity \(s_{TOT}\)
at the source position is given by:
|
$$ t_{TOT} = (2\,(2\,subscanDuration + deadTime)) \; nCrossScans $$
|
Where:
\(nCrossScans\) = total number of Cross Scans that must be executed to reach
the desired sensitivity;
\(deadTime\) = time which is not spent acquiring data during
the execution of each one of the two crosses composing a Cross Scan.
To evaluate \(t_{TOT}\) we must compute: \(deadTime\), \(subscanDuration\) and
\(nCrossScans\).
- Evaluate deadTime:
The parameter \(deadTime\) is the time which is not spent acquiring data during
the execution of each one of the two crosses composing a Cross Scan. It is
given by the sum of two terms:
\(interSubscanTime\) and \(intraSubscanTime\).
The first term is given by the duration of the
acceleration/deceleration ramps taking place before/after the actual subscans,
and is determined as a function of the scanning speed and of a given
fraction of the maximum acceleration allowed by the mount, specific for each
telescope.
For Medicina and SRT we consider the maximum acceleration MaxAcc to be
\({\bf 0.4^{\circ} / s^2}\) and \({\bf 0.25^{\circ} / s^2}\) respectively,
and we use
one tenth of the maximum acceleration to compute the ramps
(as the system itself does, to guarantee the maximum precision):
|
$$ rampTime = \frac{speed}{0.1 \, MaxAcc} $$
|
The execution of each subscan implies to perform 2 ramps, so:
|
$$ interSubscanTime = \frac{2\, speed}{0.1 \, MaxAcc} $$
|
The term \(intraSubscanTime\) is an indicative intra-scan slewing time
(i.e. performed at full \(MaxAcc\)),
which takes into account the change in position among subscans. By reverting
the formula for the uniformly accelerated motion
(\(s = \frac{1}{2} \, a \, t^2\)) and considering that \(s\) (the intra-scan path)
in this case is the hypotenuse of a triangle whose sides are the two
half-subscans:
|
$$ intraSubscanTime = \sqrt{\frac{\sqrt{2} \; subScanLength}{MaxAcc}} $$
|
It is now possible to estimate the overall dead time for one cross in a Cross
Scan: it
is given by twice the \(interSubscanTime\) (two sub-scans form one Cross Scan)
plus once the \(intraSubscanTime\) (the telescope changes position between
subscans once per Cross Scan).
|
$$ deadTime = 2 \; interSubscanTime + intraSubscanTime $$
|
- Evaluate subscanDuration:
The duration of a single subscan is easily computed as:
|
$$ subscanDuration = subscanLength \; / \; scanSpeed $$
|
- Evaluate nCrossScans:
First compute \(t_{TOT,sample}\) = time necessary to reach the desired
sensitivity \(s_{TOT}\) by using the radiometer formula (inclusive of the Real
World factor if appropriate):
|
$$t_{TOT,sample} = \left(\frac{T_{sys}}{G \; s_{TOT}}\right)^2
\frac{1}{totBand}$$
|
Given the sample interval, the number of subscans to be performed to reach
the requried sensitivity at the source position is:
|
$$ nSubscans = \frac{t_{TOT,sample}}{sampleInterval} $$
|
The number of complete Cross Scans is:
|
$$ nCrossScans = (nsubscans)/4$$
|
This value is rounded up to the upper integer.
CASE B: GIVEN \({\bf t_{TOT}}\) COMPUTE \({\bf s_{TOT}}\)
The parameter \(t_{TOT}\) is the overall observing time and thus includes also
\(deadTime\).
The actual sensitivity \(s_{TOT}\) is computed starting
from the effective time
spent on Cross Scans, i.e. excluding \(intraSubscanTime\) and \(interSubscanTime\).
First we need to compute how many Cross Scans can be executed in the given
\(t_{TOT}\):
|
$$ nCrossScans = \frac{t_{TOT}}{singleCrossTotalTime} $$
|
where \(singleCrossTotalTime\) is the total time to execute one Cross Scan
(including its overheads):
|
$$ singleCrossTotalTime = 2\, (2 \, subscanDuration + deadTime) $$
|
and \(deadTime\) is computed as in Case A. The value of \(nCrossScans\)
is rounded to the upper integer.
The sensitivity associated to an integration time equal to the sampling
interval can be computed using the radiometer formula:
|
$$s_{subScan} = \left(\frac{T_{sys}}{ G}\right) \;
\sqrt{\frac{1}{totBand \; \times \; sampleInterval}} $$
|
Then the sensitivity \(s_{TOT}\) at the source position is obtained from the
instantaneous sensitivity and the number of subscans in a Cross Scan:
|
$$ s_{TOT} =\frac{1}{\sqrt{4 \times nCrossScans}} \;
s_{subScan} $$
|
When selecting the On-The-Fly Cross Scan computations, the following
paramenters are given in output:
-
Receiver gain, system temperature and beam HPBW from tabulated values for the
seleted receiver.
- Actual elevation used for computations: this parameter may sligthly
differ from the user-selected one. Values for \(T_{sys}\) are tabulated
at different values of the elevation, typically every 5 degrees. Among the
tabulated values, the ETC looks for the \(T_{sys}\) which was measured at the
elevation closest to the user-selected one.
- Estimate of the Confusion Noise at the selected frequency (not implemented
for Medicina).
- Total Time and Sensitivity for 1 Cross Scan. These are the time needed to
complete 1 Cross Scan and the sensitivity that can be reached at the source
position in 1 Cross Scan. They are computed, according
to the quantities derived above, as
\(singleCrossTotalTime\) and
\(singleCrossRms = s_{TOT} \;/ \; \sqrt{nCrossScans}\).
- Total N. of Cross Scans: the number of Cross Scans \(nCrossScans\)
(each one being made of a couple of orthogonal subScans) to be executed and
combined in order to reach the desired input sensitivity / exposure time.
A minimum of 2 Cross Scans is imposed.
- Total dead Time is the dead time spent for the execution of the required
number of Cross Scans, i.e. \(deadTime \times nCrossScans\). It takes into
account the slewing time plus the acceleration/deceleration ramps.
- Total OTF Cross Scan Time is the total observing time needed to reach
the user-selected sensitivity over \(nCrossScans\) Cross Scans. Conversely,
Total OTF Cross Scan sensitivity is the sensitivity obtained over
\(nCrossScans\) Cross Scans given the user-selected observing time.
- Effective Total OTF Cross Scan Time or Effective Total OTF Cross Scan
sensitivity. Due to the need to make some approximation (f.i. the Cross Scan
geometry requires that an even number of subscans is executed), the effective
total
sensitivity or the effective total time are re-computed, starting from the
desired ones and taking into account the observing setup. Effective values
may slightly differ from the input requested values because of the above
approximations.
Each map is composed by a sequence of back-and-forth On-The-Fly subscans. Each
subscan is shifted with respect to the previous one in order to fully cover
the desired sky region.
An example of On-The-Fly Map geometry is shown in the following Figure, where
each arrow represent a subscan.

ETC computations are done always considering one feed, even if a multifeed
receiver (like the K-band one at SRT and Medicina) is selected.
For OTF Map computations the user provides in input:
1) the scan speed at which the telescope moves during the Cross Scan:
\(scanSpeed\) (arcmin/sec, equivalent to deg/min);
2) the time interval between two subsequent samples:
\(sampleInterval\) (sec);
3) the map edge, i.e. the map span on each side of the source, expressed
in n. of HPBW: \(mapEdge\). The source size and \(mapEdge\) are
used to compute the size of the map (see computations below).
4) the number of scans for each HPBW, corresponding to the HPBW sampling:
\(linesPerHPBW\).
5) source parameters:
- source geometry: extended or pointlike;
- source flux: \(Flux\) it must be given in mJy/beam for pointlike sources
or in mJy for extended sources (intended as the source integrated flux).
Flux values are only used to compute the total S/N;
- source sizes: for extended sources \(size_x\), \(size_y\) (arcmin).
The size of pointlike sources is set by default to the HPBW value for the
selected receiver. The source size and \(mapEdge\) are
used to compute the size of the map.
6) the desired total sensitivity over one HPBW, i.e. the sensitivity to be
reached over an HPBW area, \(s_{TOT}\) (mJy/beam). In this case the ETC
computes how many OTF maps are needed to reach that sensitivity.
Alternatively, one can provide
the total time to be spent in OTF map mode with the selected
observing setup, \(t_{TOT}\) (sec). In this case the ETC computes how many
maps will be completed in that time interval and what value of the final
sensitivity is going to be reached.
IMPORTANT NOTES:
1) if the user provides a sensitivity and wants to know the time necessary to
reach it, the sensitivity is intended to be reached over an HPBW by performing
OTF map observations for a duration equal to the computed time.
That means time is not on-source, but is the overall duration of the
observation including "dead time" (a priori known).
Accordingly, if the user provides a time and wants to know to which sensitivity
it corresponds, time is intended as the total time needed to perform all the
map observations necessary to reach the given sensitivity over an HPBW,
including "dead time".
2) Due to the need to make some approximation (f.i. the requirment that at
least 1 map is to be executed), the effective total sensitivity or the
effective total time are re-computed, starting from the desired ones
and taking into account the observing setup. Effective values may slightly
differ from the input requested values because of the above approximations.
CASE A: GIVEN \({\bf s_{TOT}}\) COMPUTE \({\bf t_{TOT}}\)
The time \(t_{TOT}\) can be expressed as:
|
$$ t_{TOT} = n_{map} * t_1 $$
|
where:
\(n_{map}\) = number of maps to be combined to reach \(s_{TOT}\).
\(t_1\) = time needed to complete one map given the observing parameters,
including dead time.
To evaluate \(t_{TOT}\) we must compute: \(n_{map}\) and \(t_1\).
- Evaluate \({\bf n_{map}}\):
The expression for \(s_{TOT}\) can be written as:
|
$$ s_{TOT} = \frac{s_1}{\sqrt{n_{map}}} $$
|
Where \(s_1\): sensitivity reached over one HPBW in a single map assuming
that each beam size is sampled with \(linesPerHPBW\) points (i.e. \(linesPerHPBW\)
scans are needed to sample one HPBW). It can be easily computed by means
of the sensitivity per HPBW reached in a single subscan:
|
$$ s_1 = \frac{sensitivityHPBW_{singlesubscan}}{\sqrt{linesPerHPBW}} $$
|
where the formula for \(sensitivityHPBW_{singlesubscan}\) is the same as in the
OTF Cross Scan case.
By substituting \(s_1\) and \(s_{TOT}\) in the above formula, the number of maps
\(n_{maps}\) can be evaluated.
- Evaluate \({\bf t_1}\):
The time needed to complete 1 map, including dead time, is:
|
$$ t_1 = (t_{singleScan} + deadTime) \; linesPerMap $$
|
where:
|
$$ t_{singleScan} = mapSize \; / \; scanSpeed $$
|
|
$$ linesPerMap = \frac{mapSize}{HPBW} \; linesPerHPBW $$
|
and \(deadTime\) in this case is:
|
$$ deadTime = interSubscanTime + intraSubscanTime $$
|
where now, differently to what happend in the OTF Cross Scan case, the path to
be performed in uniformly accelerated motion is exactly given by the
transverse distance between two subscans (no more need to build a triangle).
The parameter intraSubscanTime is thus:
\(intraSubscanTime = \sqrt{\frac{HPBW}{linesPerHPBW} \; \frac{2}{MaxAcc}}\)
Note that in the formula for \(t_1\) we make an approximation which has a
negligible effect on the computation: the correct one would be
\(t_1 = (t_{singleScan} + interSubscanTime) \, linesPerMap +
intraSubscanTime \, (linesPerMap-1)\) since the last subscan does not require
additional turning time once completed.
Map size for pointlike sources is:
|
$$ mapSize = HPBW + 2\,(mapEdge \times HPBW) $$
|
While for extended sources:
| if \(size_x>HPBW\) or \(size_y>HPBW\): |
\( mapSize = [max(size_x,size_y)] + 2\,(mapEdge \times HPBW) \) |
| if \(size_x \le HPBW\) and \(size_y \le HPBW\): |
\( mapSize = HPBW + 2\,(mapEdge \times HPBW) \) |
Finally, the Signal to Noise ratio over 1 HPBW area on the combined nmap is
computed as:
| pointlike sources: |
$$\frac{S}{N} = \frac{Flux}{s_{TOT}} $$ |
| extended sources: |
$$\frac{S}{N} = \left(\frac{Flux \times HPBWarea}{sourceArea}\right) \frac{1}{s_{TOT}}$$ |
where:
| $$ sourceArea = \pi \times 0.5 \, size_x \times 0.5 \, size_y $$ |
| $$ HPBWarea = \pi \times (0.5 \, HPBW)^2 $$ |
NOTE that the formula for extended sources gives an approximated result when
\(size_x\) or \(size_y\) is sensibly smaller than \(HPBW\) i.e. the source is
elongated and it actually does not fill "well" the beam. Results are accurate
if the extended source completely fills the beam in both directions.
CASE B: GIVEN \({\bf t_{TOT}}\) COMPUTE \({\bf s_{TOT}}\)
The parameter \(t_{TOT}\) is the overall observing time and thus includes also
\(deadTime\).
The actual sensitivity \(s_{TOT}\) must be computed using the effective time
spent on the map, i.e. excluding \(intraSubscanTime\) and \(interSubscanTime\).
First we need to compute how many maps can be executed in the given
\(t_{TOT}\), rounded to nearest integer (and at least equal to 1):
|
$$ nMaps = {\rm (nearest \;integer)}(t_{TOT} \; / \; t_1) $$
|
where \(t_1\) is the time needed to complete one map given the observing
parameters, including dead time, and is computed as in Case A.
The sensitivity \(s_{TOT}\) is thus computed as:
|
$$ s_{TOT} = \frac{s_1}{\sqrt{nMaps}} $$
|
Where \(s_1\) is the sensitivity reached over one HPBW in a single map,
computed as in Case A.
When selecting the On-The-Fly Map computations, the following
paramenters are given in output:
-
Receiver gain, system temperature and beam HPBW from tabulated values for the
seleted receiver.
- Actual elevation used for computations: this parameter may sligthly
differ from the user-selected one. Values for \(T_{sys}\) are tabulated
at different values of the elevation, typically every 5 degrees. Among the
tabulated values, the ETC looks for the \(T_{sys}\) which was measured at the
elevation closest to the user-selected one.
- Estimate of the Confusion Noise at the selected frequency (not implemented
for Medicina).
- Map size: maps are defined as squares centered on the source.
Depending on the source geometry, the map size \(mapSize\) is computed according
to the above formulae.
- N. of subscans per map: depending on map and beam sizes and on the
desired number of scans per HPBW the parameter \(linesPerMap\) is computed.
- Total Time and Sensitivity for 1 Map. These are the quantities \(t_1\) and
\(s_1\) and refer to the time needed to complete one single map and to
the sensitivity than can be reached on a single map.
- Total N. of Maps: the number of maps \(nMaps\)
(each one being made of \(linesPerMap\) subscans) to be executed and combined
in order to reach the
desired input sensitivity / exposure time. A minimum of 1 map is imposed.
- Total dead Time is the dead time spent for the execution of the required
number of Maps, i.e. \(deadTime \times nMaps\). It takes into
account the slewing time plus the acceleration/deceleration ramps. The
parameter \(deadTime\) is computed in a sligthly different way than for
the OTF Cross Scan case, see computations above.
- Total OTF Map Time is the total observing time needed to reach
the user-selected sensitivity over \(nMaps\) OTF maps. Conversely,
Total OTF Map sensitivity is the sensitivity obtained over
\(nMaps\) OTF maps given the user-selected observing time.
- Effective Total OTF Map Time or Effective Total OTF Map
sensitivity. Due to the need to make some approximation (f.i. the
requirment that at least 1 map is to be executed), the effective total
sensitivity or the effective total time are re-computed, starting from the
desired ones
and taking into account the observing setup. Effective values may slightly
differ from the input requested values because of the above approximations.
-
Source Signal-to-Noise Ratio over 1 HPBW area on the combined final map.
This is the signal-to-noise ratio \(\frac{S}{N}\) over \(nMaps\) combined maps
and inside a circular
area of HPBW diameter. Depending on source geometry, it is computed
in terms of source flux density and total sensitivity.
Currently, confusion noise computations are implemented for SRT only.
The rms width of the point-source confusion amplitude distribution calculated
by Condon (1974) at the generic frequency \(\nu\) is:
|
$$\sigma_{c,\nu} =
\left(\frac{q^{3-\gamma}}{3-\gamma}\right) ^{\frac{1}{\gamma-1}}
\left(\frac{k \Omega_{b}}{\gamma -1}\right) ^{\frac{1}{\gamma-1}}
\left(\frac{\nu}{\nu_{0}}\right) ^{-\alpha}$$
|
Where \(q\) is the signal-to-noise ratio under which we expect confusion,
\(\Omega_{b}\) the beam solid angle, \(\alpha\) the spectral index
(with \(S = S_{0} \nu^{-\alpha}\)), and \(k\) and
\(\gamma\) are the parameters of the power-law differential source
counts calculated at the frequency \(\nu_0\):
|
$$ n_{\nu_{0}}(S) = k S^{-\gamma}$$
|
Note that for the ETC computations we assumed q = 5.
To calculate the rms confusion at various frequencies the following power-law
differential counts have been used:
-
at 1.4 GHz we used the distribution given by Bondi et al. (2003) for \(S>0.6\)
mJy:
|
$$n_{\rm 1.4\,GHz}=(75.86\pm 1.08)\left(
\frac{S}{mJy}\right)^{-(1.79\pm 0.05)}{\rm mJy^{-1}deg^{-2}}
$$
|
-
at 5 GHz we extrapolated the confusion limit from the distribution at 1.4 GHz
given by Bondi et al. (2003) for \(S<0.6\) mJy
|
$$n_{\rm 1.4\,GHz}=(57.54\pm 1.07)\left(
\frac{S}{mJy}\right)^{-(2.28\pm 0.04)}{\rm mJy^{-1}deg^{-2}}
$$
|
-
at 20 GHz, we extrapolated the confusion limit from the distribution at 15 GHz
given by Davies et al. (2011) for \( 0.5 {\rm mJy} < S < 2.8 {\rm mJy}\):
|
$$n_{\rm 15\,GHz}=376\left(\frac{S}{Jy}\right)^{-1.80}{\rm Jy^{-1}sr^{-1}}
$$
|
-
at 327 MHz, we extrapolated the confusion limit from the distribution at
333 MHz obtained by fitting the differential normalized source counts versus
the flux given by Owen et al. (2009):
|
$$n_{333 {\rm MHz}} = 1546 \left(\frac{S}{{\rm Jy}}\right)^{-1.88}
{\rm Jy^{-1} {\rm sr}^{-1}}$$
|
REFERENCES:
Bondi, M., Ciliegi, P., Zamorani, G., et al. 2003, A&A, 403, 857.
Condon, J. J. 1974, ApJ, 188, 279.
Davies, M. L., Franzen, T. M. O., et al. 2011, MNRAS, 415, 2708.
Owen, F. N., Morrison, G. E., Klimek, M. D., & Greisen, E. W. 2009, AJ,
137, 4846.


